Stack Manipulation

In this section we describe the AIR constraints for Miden VM stack manipulation operations.

PAD

The PAD operation pushes a $0$ onto the stack. The diagram below illustrates this graphically.

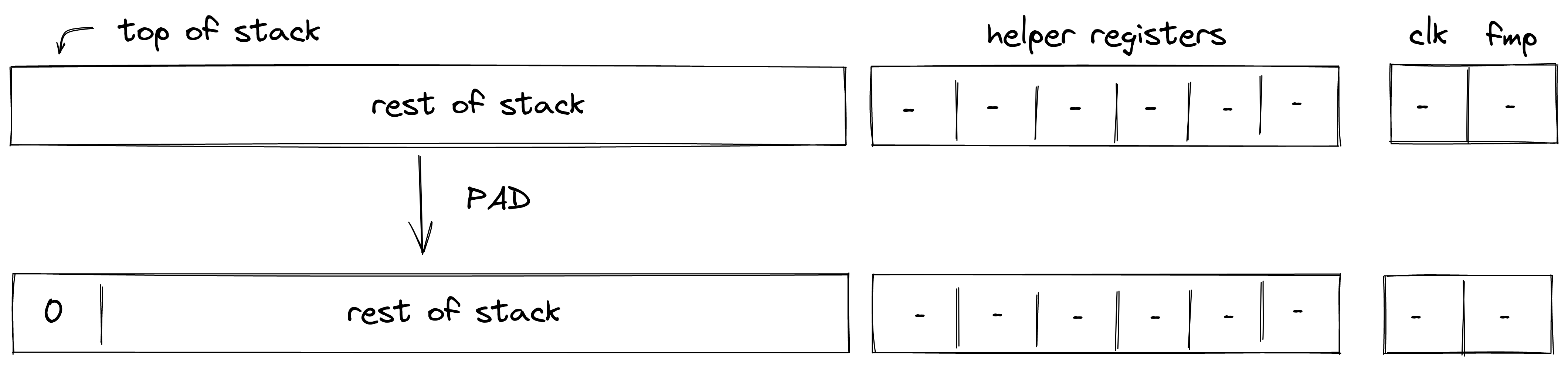
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }=0\text{ | degree}=1$$

The effect of this operation on the rest of the stack is:

• Right shift starting from position $0$.

DROP

The DROP operation removes an element from the top of the stack. The diagram below illustrates this graphically.

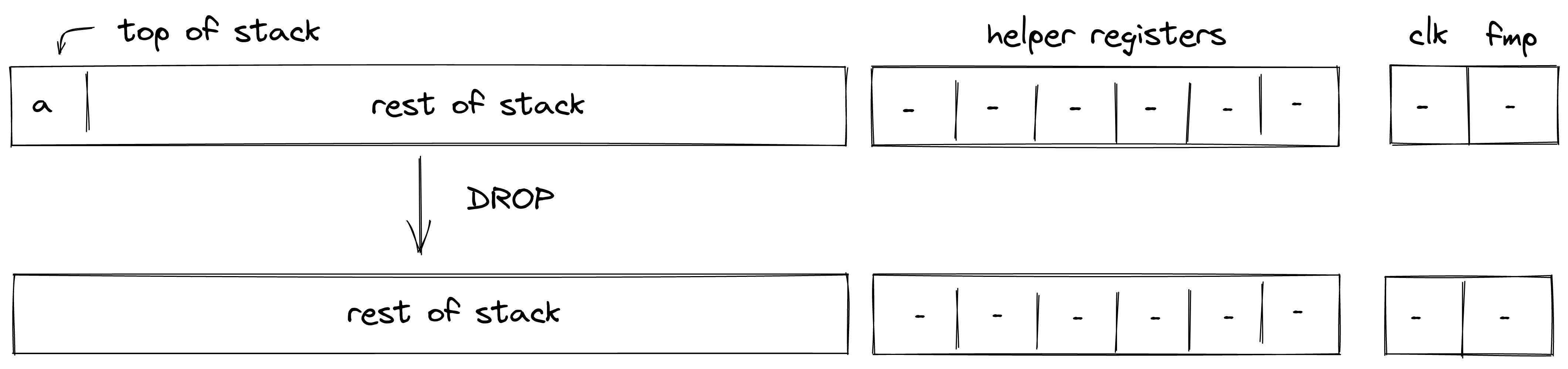
The DROP operation shifts the stack by $1$ element to the left, but does not impose any additional constraints. The degree of left shift constraints is $1$.

The effect of this operation on the rest of the stack is:

• Left shift starting from position $1$.

DUP(n)

The DUP(n) operations push a copy of the $n$-th stack element onto the stack. Eg. DUP (same as DUP0) pushes a copy of the top stack element onto the stack. Similarly, DUP5 pushes a copy of the $6$-th stack element onto the stack. This operation is valid for $n\in \{0,...,7,9,11,13,15\}$. The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-s_n=0\text{ for }n\in \{0,...,7,9,11,13,15\}\text{ | degree}=1$$

where $n$ is the depth of the stack from where the element has been copied.

The effect of this operation on the rest of the stack is:

• Right shift starting from position $0$.

SWAP

The SWAP operations swaps the top two elements of the stack. The diagram below illustrates this graphically.

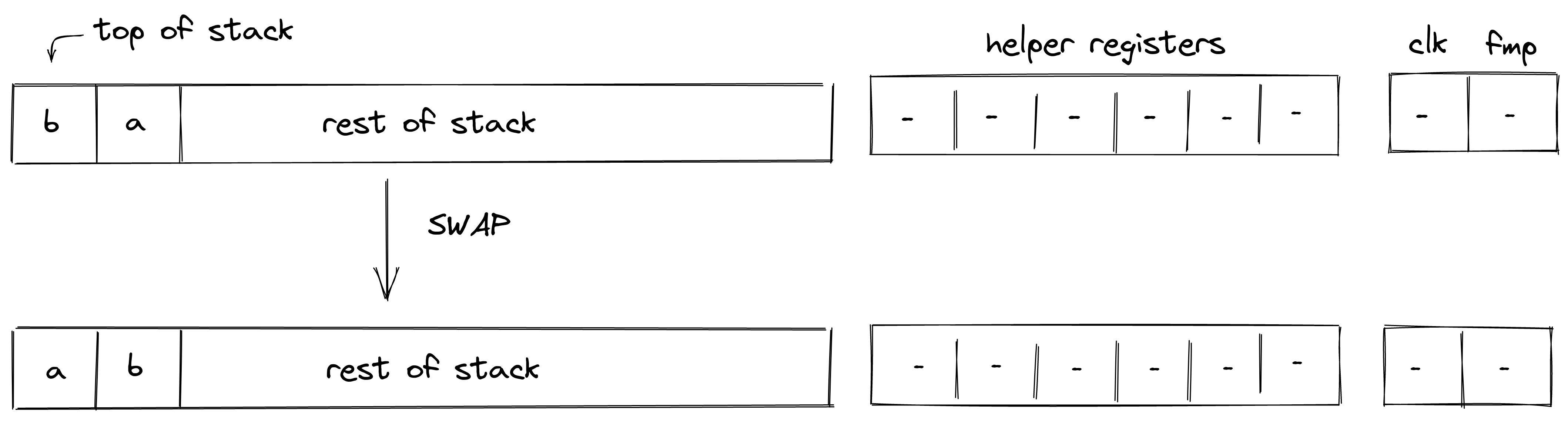
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-s_1=0\text{ | degree}=1$$

$$s_1^{\prime }-s_0=0\text{ | degree}=1$$

The effect of this operation on the rest of the stack is:

• No change starting from position $2$.

SWAPW

The SWAPW operation swaps stack elements $0,1,2,3$ with elements $4,5,6,7$. The diagram below illustrates this graphically.

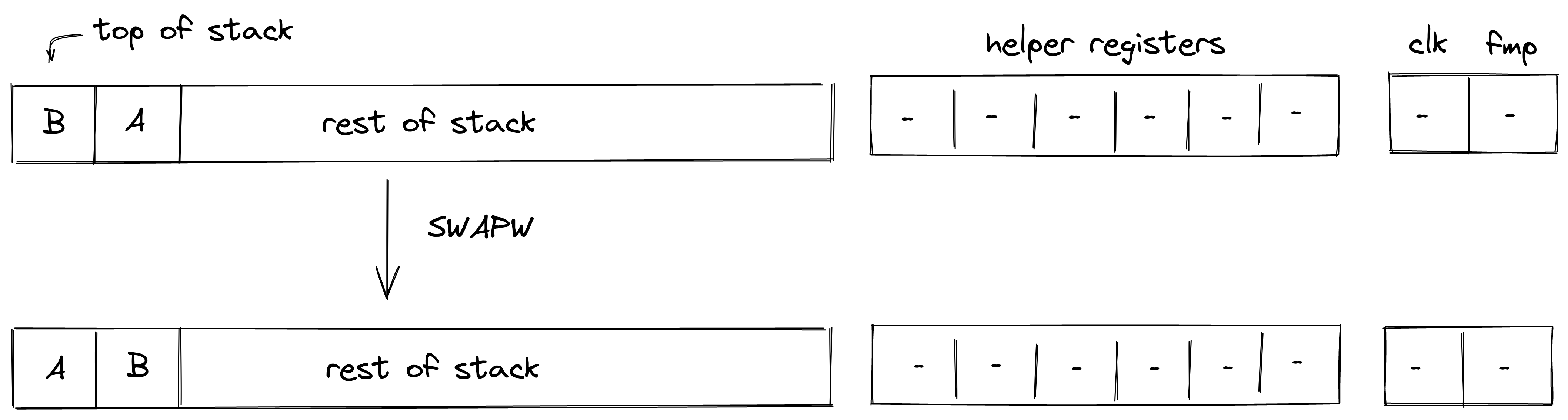
Stack transition for this operation must satisfy the following constraints:

$$s_i^{\prime }-s_{i+4}=0\text{ for }i\in \{0,1,2,3\}\text{ | degree}=1$$

$$s_{i+4}^{\prime }-s_i=0\text{ for }i\in \{0,1,2,3\}\text{ | degree}=1$$

The effect of this operation on the rest of the stack is:

• No change starting from position $8$.

SWAPW2

The SWAPW2 operation swaps stack elements $0,1,2,3$ with elements $8,9,10,11$. The diagram below illustrates this graphically.

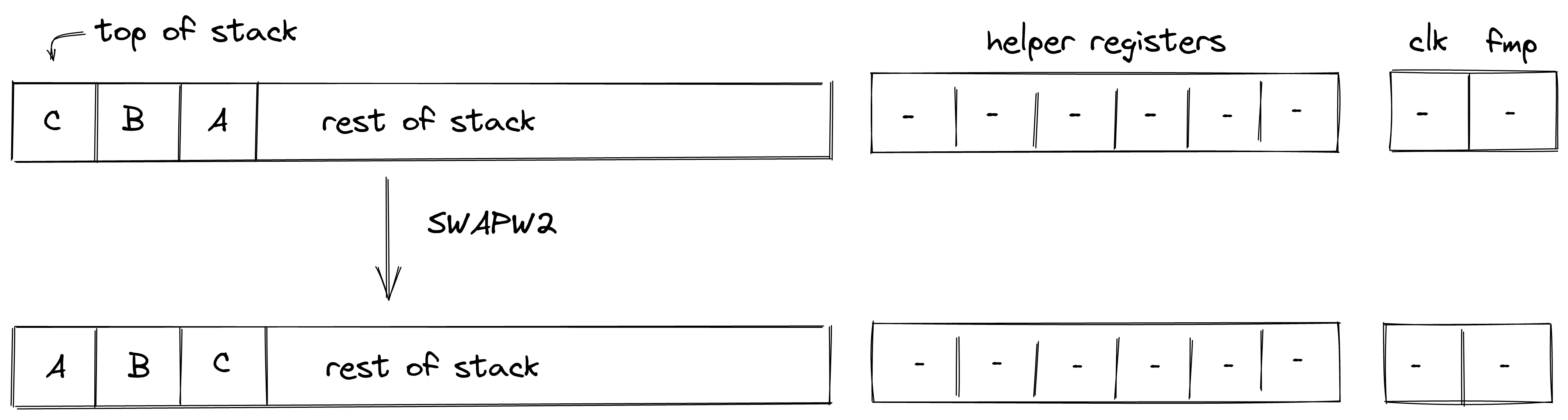
Stack transition for this operation must satisfy the following constraints:

$$s_i^{\prime }-s_{i+8}=0\text{ for }i\in \{0,1,2,3\}\text{ | degree}=1$$

$$s_{i+8}^{\prime }-s_i=0\text{ for }i\in \{0,1,2,3\}\text{ | degree}=1$$

The effect of this operation on the rest of the stack is:

• No change for elements $4,5,6,7$.
• No change starting from position $12$.

SWAPW3

The SWAPW3 operation swaps stack elements $0,1,2,3$ with elements $12,13,14,15$. The diagram below illustrates this graphically.

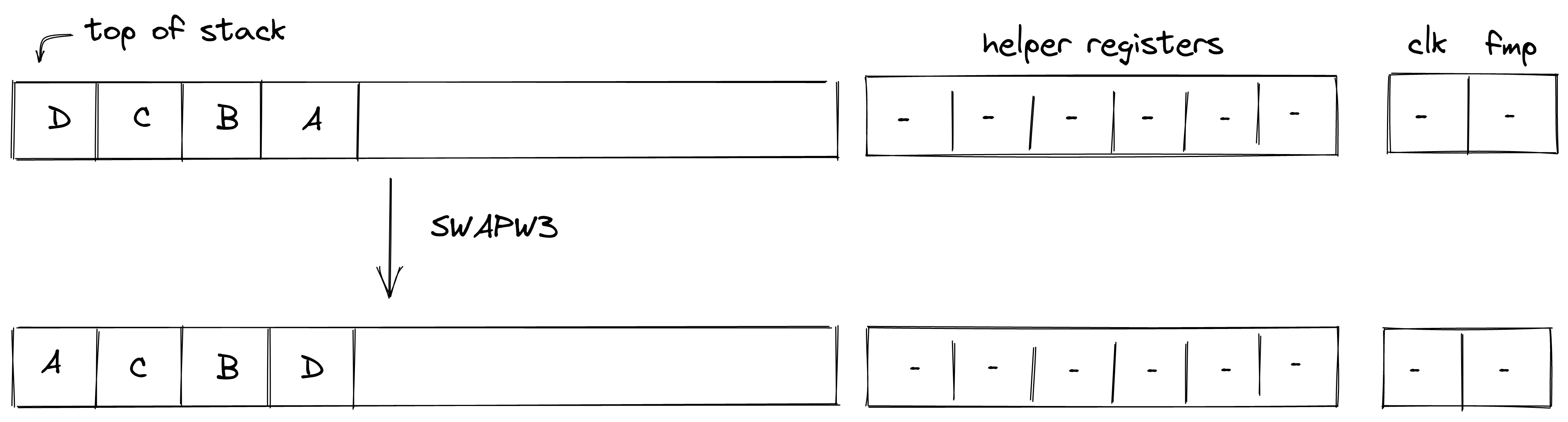
Stack transition for this operation must satisfy the following constraints:

$$s_i^{\prime }-s_{i+12}=0\text{ for }i\in \{0,1,2,3\}\text{ | degree}=1$$

$$s_{i+12}^{\prime }-s_i=0\text{ for }i\in \{0,1,2,3\}\text{ | degree}=1$$

The effect of this operation on the rest of the stack is:

• No change for elements $4,5,6,7,8,9,10,11$.
• No change starting from position $16$.

SWAPDW

The SWAPDW operation swaps stack elements $[0,8)$ with elements $[8,16)$. The diagram below illustrates this graphically.

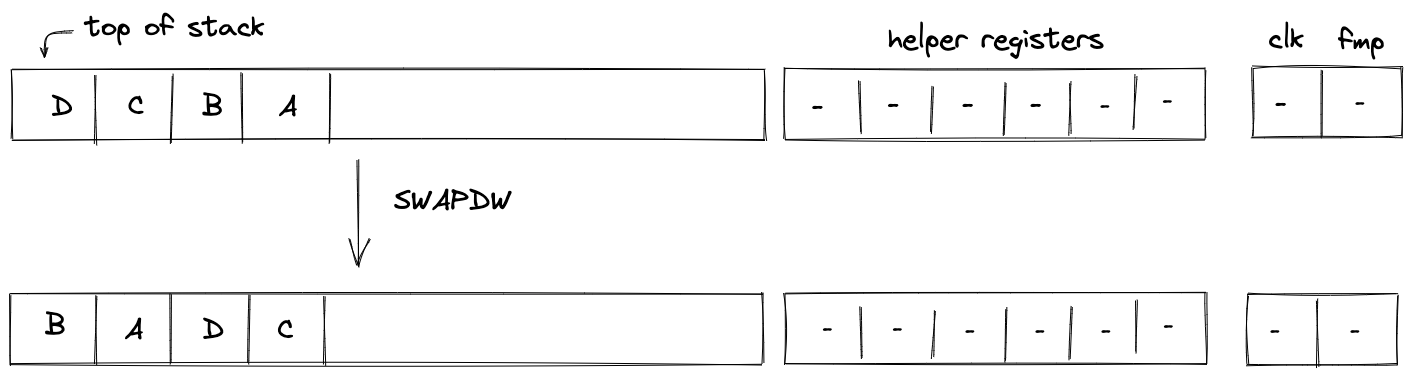
Stack transition for this operation must satisfy the following constraints:

$$s_i^{\prime }-s_{i+8}=0\text{ for }i\in [0,8)\text{ | degree}=1$$

$$s_{i+8}^{\prime }-s_i=0\text{ for }i\in [0,8)\text{ | degree}=1$$

The effect of this operation on the rest of the stack is:

• No change starting from position $16$.

MOVUP(n)

The MOVUP(n) operation moves the $n$-th element of the stack to the top of the stack. For example, MOVUP2 moves element at depth $2$ to the top of the stack. All elements with depth less than $n$ are shifted to the right by one, while elements with depth greater than $n$ remain in place, and the depth of the stack does not change. This operation is valid for $n\in [2,9)$. The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-s_n=0\text{ for }n\in [2,9)\text{ | degree}=1$$

where $n$ is the depth of the element which is moved moved to the top of the stack.

The effect of this operation on the rest of the stack is:

• Right shift for elements between $0$ and $n-1$.
• No change starting from position $n+1$.

MOVDN(n)

The MOVDN(n) operation moves the top element of the stack to the $n$-th position. For example, MOVDN2 moves the top element of the stack to depth $2$. All the elements with depth less than $n$ are shifted to the left by one, while elements with depth greater than $n$ remain in place, and the depth of the stack does not change. This operation is valid for $n\in [2,9)$. The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_n^{\prime }-s_0=0\text{ for }n\in [2,9)\text{ | degree}=1$$

where $n$ is the depth to which the top stack element is moved.

The effect of this operation on the rest of the stack is:

• Left shift for elements between $1$ and $n$.
• No change starting from position $n+1$.

CSWAP

The CSWAP operation pops an element off the stack and if the element is $1$, swaps the top two remaining elements. If the popped element is $0$, the rest of the stack remains unchanged. The diagram below illustrates this graphically.

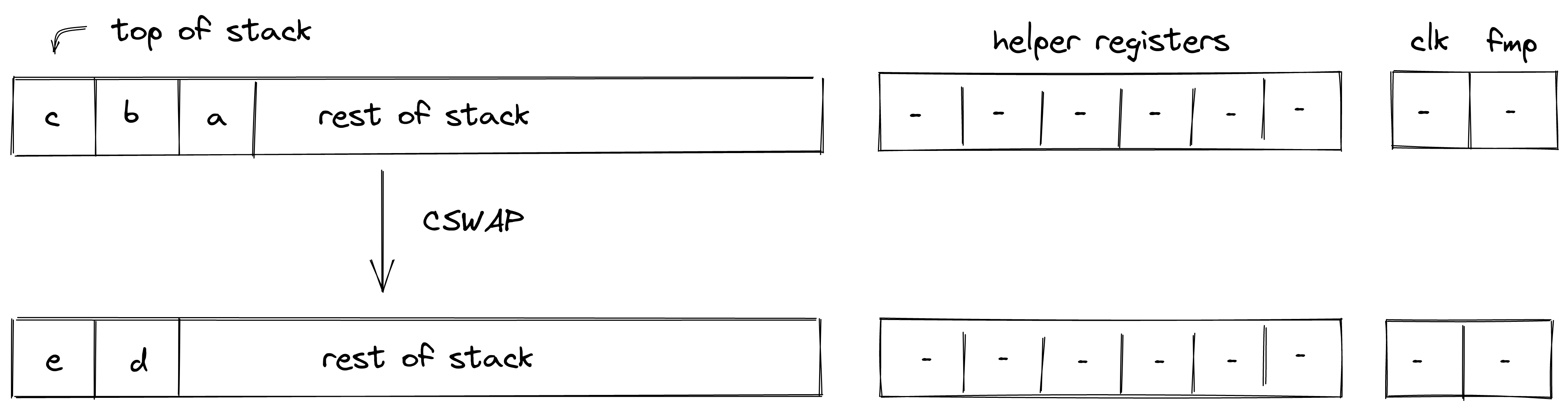
In the above:

$$d=\{\begin{array}{ll}a,& \text{if}c=0\\ b,& \text{if}c=1\end{array}e=\{\begin{array}{ll}b,& \text{if}c=0\\ a,& \text{if}c=1\end{array}$$

Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-s_0\cdot s_2-(1-s_0)\cdot s_1=0\text{ | degree}=2$$

$$s_1^{\prime }-s_0\cdot s_1-(1-s_0)\cdot s_2=0\text{ | degree}=2$$

We also need to enforce that the value in $s_0$ is binary. This can be done with the following constraint:

$$s_0^2-s_0=0\text{ | degree}=2$$

The effect of this operation on the rest of the stack is:

• Left shift starting from position $3$.

CSWAPW

The CSWAPW operation pops an element off the stack and if the element is $1$, swaps elements $1,2,3,4$ with elements $5,6,7,8$. If the popped element is $0$, the rest of the stack remains unchanged. The diagram below illustrates this graphically.

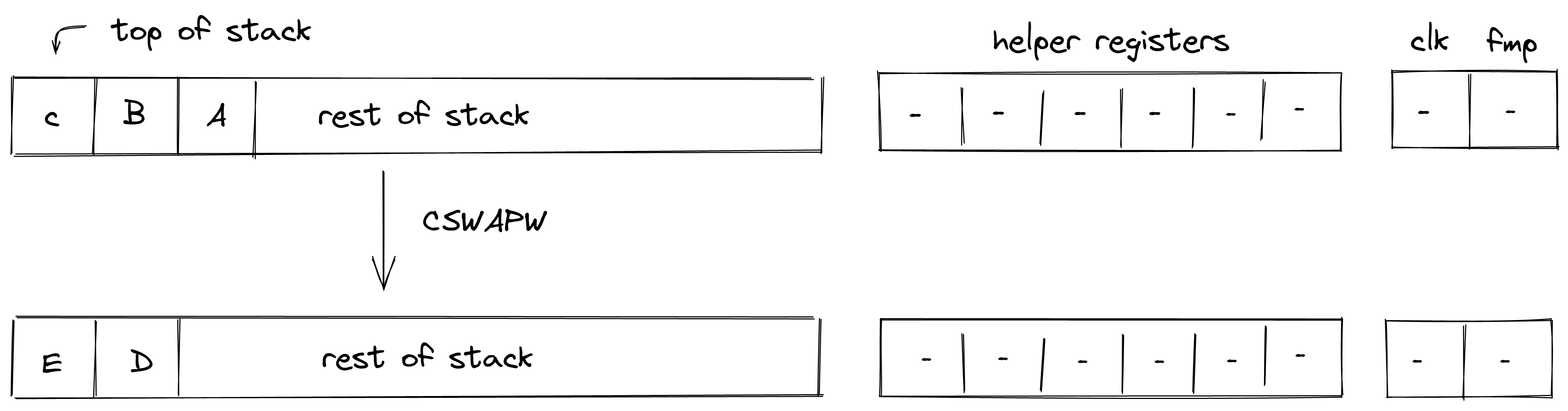
In the above:

$$D=\{\begin{array}{ll}A,& \text{if}c=0\\ B,& \text{if}c=1\end{array}E=\{\begin{array}{ll}B,& \text{if}c=0\\ A,& \text{if}c=1\end{array}$$

Stack transition for this operation must satisfy the following constraints:

$$s_i^{\prime }-s_0\cdot s_{i+5}-(1-s_0)\cdot s_{i+1}=0\text{ for }i\in [0,4)\text{ | degree}=2$$

$$s_{i+4}^{\prime }-s_0\cdot s_{i+1}-(1-s_0)\cdot s_{i+5}=0\text{ for }i\in [0,4)\text{ | degree}=2$$

We also need to enforce that the value in $s_0$ is binary. This can be done with the following constraint:

$$s_0^2-s_0=0\text{ | degree}=2$$

The effect of this operation on the rest of the stack is:

• Left shift starting from position $9$.