Field Operations

In this section we describe the AIR constraints for Miden VM field operations (i.e., arithmetic operations over field elements).

ADD

Assume $a$ and $b$ are the elements at the top of the stack. The ADD operation computes $c\leftarrow (a+b)$. The diagram below illustrates this graphically.

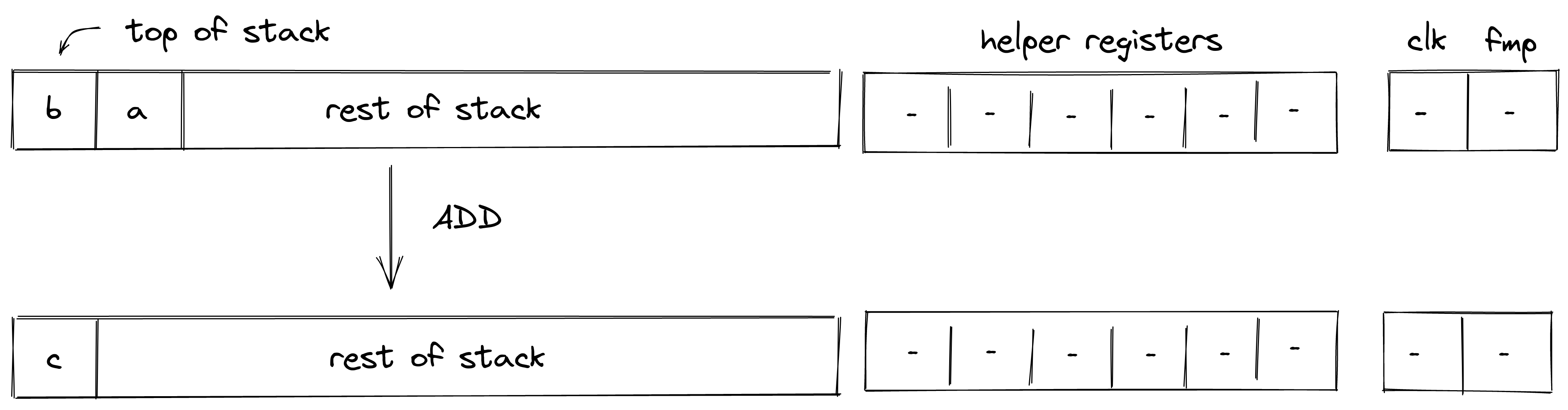
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-(s_0+s_1)=0\text{ | degree}=1$$

The effect on the rest of the stack is:

• Left shift starting from position $2$.

NEG

Assume $a$ is the element at the top of the stack. The NEG operation computes $b\leftarrow (-a)$. The diagram below illustrates this graphically.

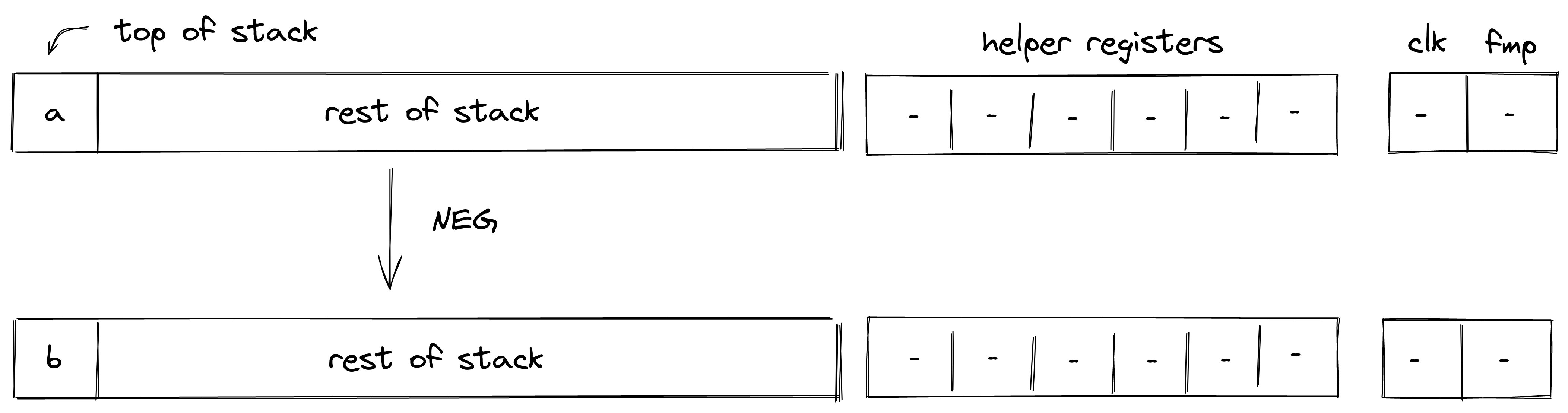
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }+s_0=0\text{ | degree}=1$$

The effect on the rest of the stack is:

• No change starting from position $1$.

MUL

Assume $a$ and $b$ are the elements at the top of the stack. The MUL operation computes $c\leftarrow (a\cdot b)$. The diagram below illustrates this graphically.

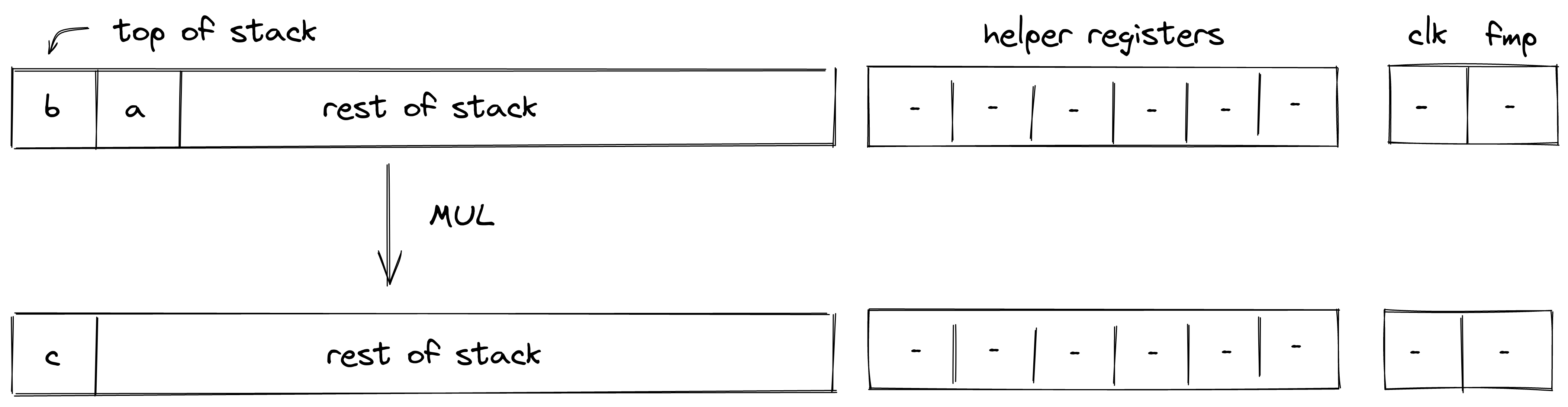
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-s_0\cdot s_1=0\text{ | degree}=2$$

The effect on the rest of the stack is:

• Left shift starting from position $2$.

INV

Assume $a$ is the element at the top of the stack. The INV operation computes $b\leftarrow (a^{-1})$. The diagram below illustrates this graphically.

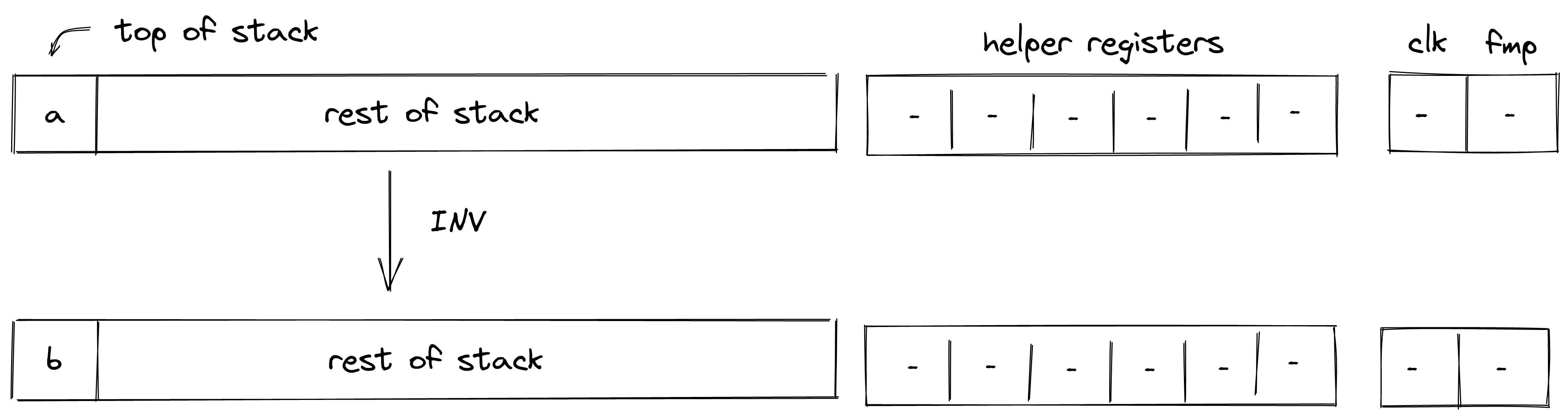
Stack transition for this operation must satisfy the following constraints:

$$1-s_0^{\prime }\cdot s_0=0\text{ | degree}=2$$

Note that the above constraint can be satisfied only if the value in $s_0\ne 0$.

The effect on the rest of the stack is:

• No change starting from position $1$.

INCR

Assume $a$ is the element at the top of the stack. The INCR operation computes $b\leftarrow (a+1)$. The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }-(s_0+1)=0\text{ | degree}=1$$

The effect on the rest of the stack is:

• No change starting from position $1$.

NOT

Assume $a$ is a binary value at the top of the stack. The NOT operation computes $b\leftarrow (\neg a)$. The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_0^2-s_0=0\text{ | degree}=2$$

$$s_0^{\prime }-(1-s_0)=0\text{ | degree}=1$$

The first constraint ensures that the value in $s_0$ is binary, and the second constraint ensures the correctness of the boolean NOT operation.

The effect on the rest of the stack is:

• No change starting from position $1$.

AND

Assume $a$ and $b$ are binary values at the top of the stack. The AND operation computes $c\leftarrow (a\wedge b)$. The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_i^2-s_i=0\text{ for }i\in \{0,1\}\text{ | degree}=2$$

$$s_0^{\prime }-s_0\cdot s_1=0\text{ | degree}=2$$

The first two constraints ensure that the value in $s_0$ and $s_1$ are binary, and the third constraint ensures the correctness of the boolean AND operation.

The effect on the rest of the stack is:

• Left shift starting from position $2$.

OR

Assume $a$ and $b$ are binary values at the top of the stack. The OR operation computes $c\leftarrow (a\vee b)$ The diagram below illustrates this graphically.

Stack transition for this operation must satisfy the following constraints:

$$s_i^2-s_i=0\text{ for }i\in \{0,1\}\text{ | degree}=2$$

$$s_0^{\prime }-(s_1+s_0-s_1\cdot s_0)=0\text{ | degree}=2$$

The first two constraints ensure that the value in $s_0$ and $s_1$ are binary, and the third constraint ensures the correctness of the boolean OR operation.

The effect on the rest of the stack is:

• Left shift starting from position $2$.

EQ

Assume $a$ and $b$ are the elements at the top of the stack. The EQ operation computes $c$ such that $c=1$ if $a=b$, and $0$ otherwise. The diagram below illustrates this graphically.

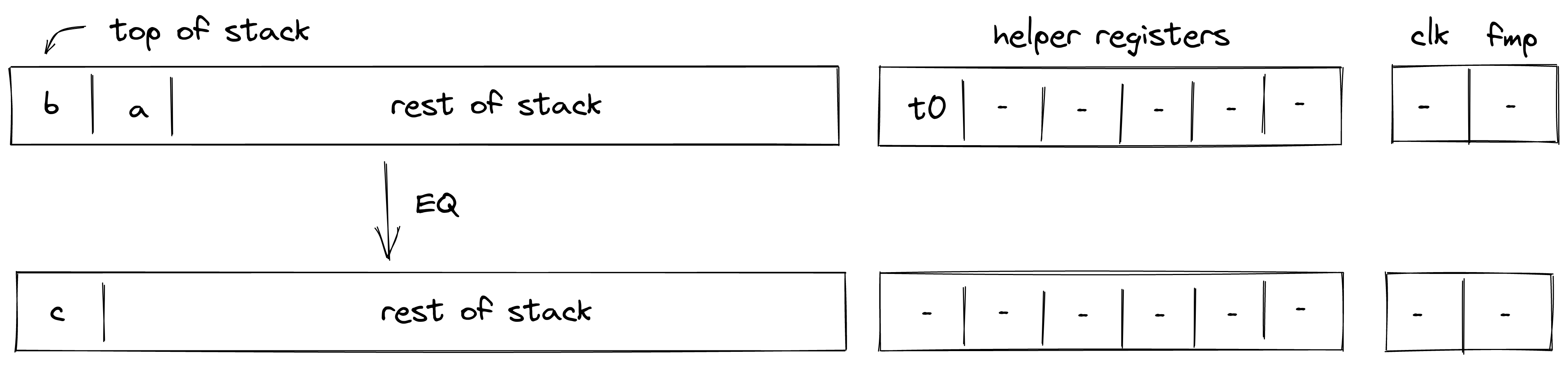
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }\cdot (s_0-s_1)=0\text{ | degree}=2$$

$$s_0^{\prime }-(1-(s_0-s_1)\cdot h_0)=0\text{ | degree}=2$$

To satisfy the above constraints, the prover must populate the value of helper register $h_0$ as follows:

• If $s_0\ne s_1$, set $h_0=\frac{1}{s_0-s_1}$.
• Otherwise, set $h_0$ to any value (e.g., $0$).

The effect on the rest of the stack is:

• Left shift starting from position $2$.

EQZ

Assume $a$ is the element at the top of the stack. The EQZ operation computes $b$ such that $b=1$ if $a=0$, and $0$ otherwise. The diagram below illustrates this graphically.

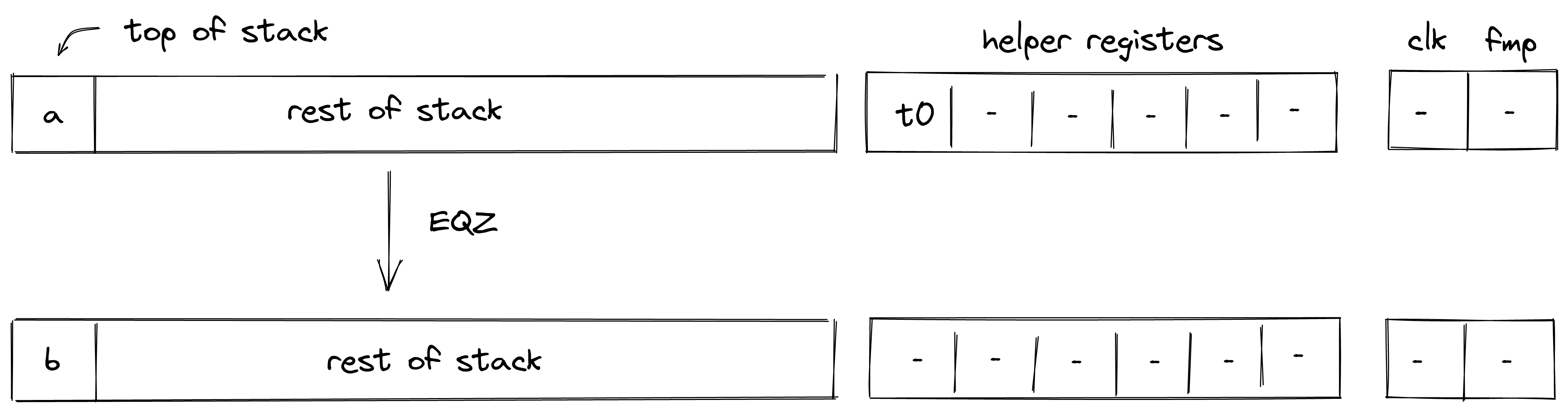
Stack transition for this operation must satisfy the following constraints:

$$s_0^{\prime }\cdot s_0=0\text{ | degree}=2$$

$$s_0^{\prime }-(1-s_0\cdot h_0)=0\text{ | degree}=2$$

To satisfy the above constraints, the prover must populate the value of helper register $h_0$ as follows:

• If $s_0\ne 0$, set $h_0=\frac{1}{s_0}$.
• Otherwise, set $h_0$ to any value (e.g., $0$).

The effect on the rest of the stack is:

• No change starting from position $1$.

EXPACC

The EXPACC operation computes one round of the expression $bas{e}^{exp}$. It is expected that Expacc is called at least num_exp_bits times, where num_exp_bits is the number of bits required to represent exp.

It pops $4$ elements from the top of the stack, performs a single round of exponent aggregation, and pushes the resulting $4$ values onto the stack. The diagram below illustrates this graphically.

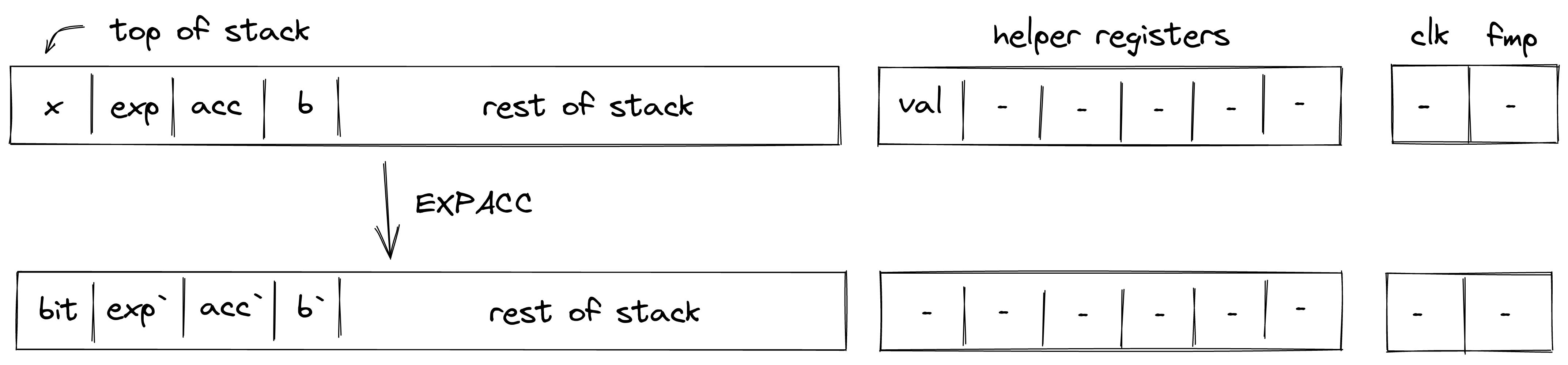
Expacc is based on the observation that the exponentiation of a number can be computed by repeatedly squaring the base and multiplying those powers of the base by the accumulator, for the powers of the base which correspond to the exponent's bits which are set to 1.

For example, take $b^5=(b^2{)}^2\cdot b$. Over the course of 3 iterations ($5$ is $101$ in binary), the algorithm will compute $b$, $b^2$ and $b^4$ (placed in base_acc). Hence, we want to multiply base_acc in acc when $bas{e}_{a}cc=b$ and when $bas{e}_{a}cc=b^4$, which occurs on the first and third iterations (corresponding to the $1$ bits in the binary representation of 5).

Stack transition for this operation must satisfy the following constraints:

bit' should be a binary.

$$s_0^{\prime 2}-s_0^{\prime }=0\text{ | degree}=2$$

The base in the next frame should be the square of the base in the current frame.

$$s_1^{\prime }-s_1^2=0\text{ | degree}=2$$

The value val in the helper register is computed correctly using the bit and exp in next and current frame respectively.

$$h_0-((s_1-1)\ast s_0^{\prime }+1)=0\text{ | degree}=2$$

The acc in the next frame is the product of val and acc in the current frame.

$$s_2^{\prime }-s_2\ast h_0=0\text{ | degree}=2$$

exp in the next frame is half of exp in the current frame (accounting for even/odd).

$$s_3^{\prime }-(s_3\ast 2+s_0^{\prime })=0\text{ | degree}=1$$

The effect on the rest of the stack is:

• No change starting from position $4$.

EXT2MUL

The EXT2MUL operation pops top $4$ values from the top of the stack, performs multiplication between the two extension field elements, and pushes the resulting $4$ values onto the stack. The diagram below illustrates this graphically.

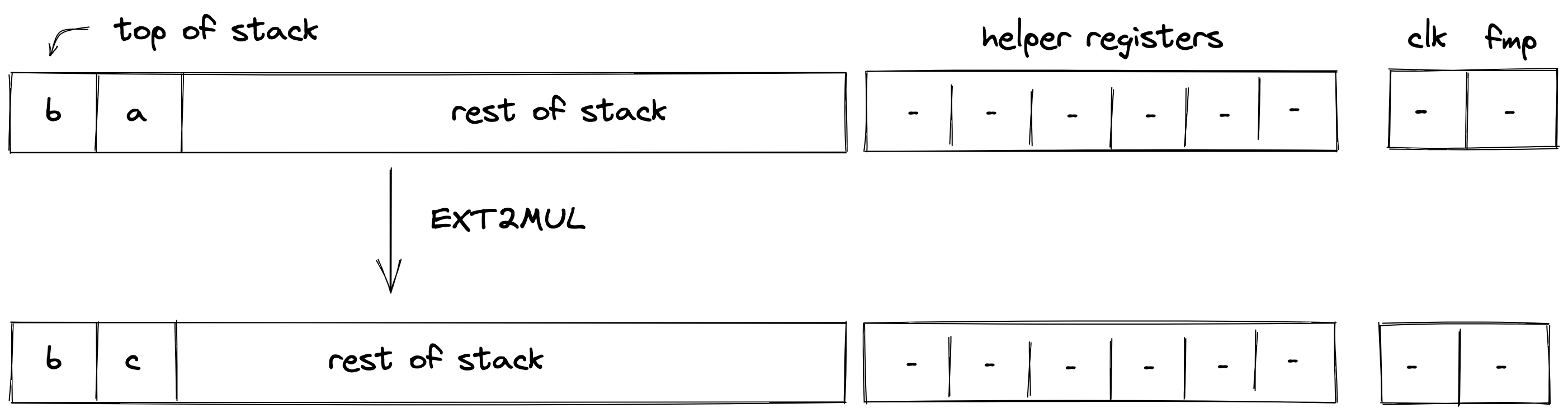
Stack transition for this operation must satisfy the following constraints:

The first stack element should be unchanged in the next frame.

$$s_0^{\prime }-s_0=0\text{ | degree}=1$$

The second stack element should be unchanged in the next frame.

$$s_1^{\prime }-s_1=0\text{ | degree}=1$$

The third stack element should satisfy the following constraint.

$$s_2^{\prime }-(s_0+s_1)\cdot (s_2+s_3)+s_0\cdot s_2=0\text{ | degree}=2$$

The fourth stack element should satisfy the following constraint.

$$s_3^{\prime }-s_1\cdot s_3+2\cdot s_0\cdot s_2=0\text{ | degree}=2$$

The effect on the rest of the stack is:

• No change starting from position $4$.